Алгоритм обратного распространения ошибки (backpropagation)
Горин Виктор
Волгоград, 2007
Скачать чтатью в pdf-формате:
 backprop.pdf (420 kb)
backprop.pdf (420 kb)
Впервые процедуру обратного распространения (не только для нейронных сетей) описал Paul J. Werbos в 1974 году в своей кандидатской диссертации, но известность алгоритм получил после публикации в 1986 году работы David E. Rumelhart, Geoffrey E. Hinton и Ronald J. Williams. За прошедшее время его актуальность не потерялась, возможно, он является наиболее часто применяемым на сегодняшний день, хотя и разработаны ускоренные алгоритмы, показывающие увеличение скорости сходимости на порядок на некоторых задачах. Более быстрые градиентные методы являются надстройками над backpropagation, как правило, используют эвристические приемы глобальной или локальной адаптации.
Рассмотрим применение алгоритма для обучения полносвязной сети прямого распространения. На рисунке 1 схематически изображена такая сеть, количество элементов в слое любое, это только на рисунке слои одного размера. Нейроны, вообще говоря, не обязаны быть одинаковыми, то есть активационная функция для каждого может быть задана индивидуально. Наиболее часто используются сигмоидные: логистическая функция и гиперболический тангенс.
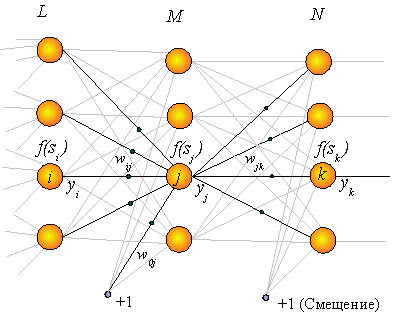 Рис. 1.
Рис. 1. Нейрон с индексом
k находится в выходном слое. Выходы нейронов
i, j, k обозначены
yi , yj , yk соответственно. Вес синапса, соединяющего нейрон
i с нейроном
j , имеет обозначение
wij , синапс, взвешивающий формальный вход
w0j ,
sj – взвешенная сумма входов нейрона
j.
Перед началом обучения веса инициализируются небольшими случайными значениями, такими, чтобы при подаче обучающих примеров нейроны не могли оказаться в насыщении. Это необходимо для того, чтобы сеть вообще могла учиться. Если все веса установить нулевыми, алгоритм работать не будет.
В процессе обучения на вход сети подаются по очереди (рекомендуется в случайном порядке) примеры из обучающего множества, поданный на вход сигнал распространяется вдоль сети (прямой проход). При прямом проходе вычисляются взвешенные суммы входов для каждого нейрона, с учетом формального входа:
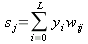 | (1) |
sj – взвешенная сумма входов нейрона
j ;
yi – выходы нейронов предыдущего слоя или, если нейрон
j находится в первом слое, то входы сети;
wij – весовой коэффициент синапса (вес), соединяющего
i-й и
j-й нейроны.
L – число нейронов в предыдущем слое. Сигнал формального входа значения не имеет, возьмем его единичным.
Выход нейрона определяется активационной функцией (для каждого может быть выбрана индивидуально), аргументом которой будет взвешенная сумма:
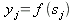 | (2) |
Теперь на выходе сети имеются сигналы
yj , которые отличаются от значений выходных образов обучающего множества. Их разница и составит ту ошибку, в зависимости от которой следует скорректировать веса всей сети.
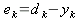 | (3) |
ek – ошибка для выходного нейрона
k, dk – желаемое значение на данном выходе (из обучающего примера).
Энергию ошибки (для данного примера, по всем выходам) запишем следующим образом:
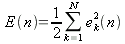 | (4) |
где
N – число нейронов в выходном слое,
n – номер подаваемого примера. Суммарную энергию ошибки (по всем примерам) можно записать:
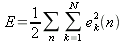 | (5) |
Это есть величина, которую будем стремиться минимизировать в процессе обучения. Нагляднее ошибку представляет средняя величина, она не зависит от числа примеров в обучающем множестве:
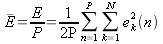 | (6) |
где
P – размер обучающего множества (количество примеров).
Итак, на выходе имеем сигнал ошибки, но эта ошибка известна только для открытого – выходного слоя, нужно распределить её по всем синапсам сети в зависимости от вклада, внесенного каждым весом. Теперь сеть работает в обратном направлении. Сигнал ошибки как бы подключается к её выходу и распространяется в направлении входов (отсюда и название алгоритма). Определять коррекцию весов
Dwij будем методом градиентного спуска, она пропорциональна частной производной и определяется дельта-правилом:
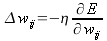 | (7) |
здесь
h – коэффициент скорости обучения (значение в интервале от 0 до 1, берут относительно небольшим, не рекомендуется более 0.1); знак «минус» означает, что подстройка весов идёт в направлении антиградиента. Используя правило цепочки, можем расписать частную производную следующим образом:
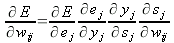 | (8) |
Пусть нам известна ошибка на выходе скрытого нейрона
j , тогда уравнение (4) можем переписать:
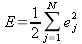 | (9) |
Продифференцируем обе части этого по
ej , получаем:
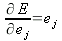 | (10) |
Пусть
dj – эталонное значение на выходе
j-го нейрона, тогда (3) можно переписать:
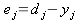 | (11) |
и, дифференцируя обе части по
yj , получим:
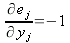 | (12) |
Дифференцируя также уравнение (2) по
sj , запишем:
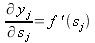 | (13) |
f '(sj) означает производную активационной функции. Для сигмоидных функций производная может быть выражена через само значение функции. Так, например, для гиперболического тангенса:
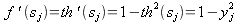 | (14) |
для логистической функции:
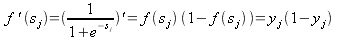 | (15) |
Теперь дифференцируем (1):
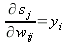 | (16) |
Подставим полученные уравнения (10), (12), (13), (16) в (8):
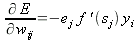 | (17) |
Можем подставить (17) в (7), для расчета коррекции имеем:
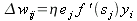 | (18) |
Локальный градиент определяется как частная производная энергии ошибки по взвешенной сумме входов:
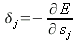 | (19) |
или, снова применяя правило цепочки:
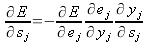 | (20) |
Подставляя ранее полученные (10), (12), (13), окончательно имеем:
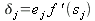 | (21) |
Тогда коррекцию можно записать в виде:
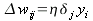 | (22) |
Итак, формулы (21), (22) можно использовать для расчета коррекции весов любого нейрона. Перепишем эти уравнения для выходного слоя:
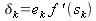 | (23) |
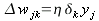 | (24) |
тут все величины могут быть получены непосредственно. Но для скрытого слоя не знаем
dj , будем искать из значений, найденных для верхних слоев. Для этого, вновь воспользовавшись правилом цепочки, запишем (19) для скрытого нейрона:
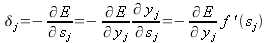 | (25) |
Энергия ошибки сети уже была записана в (4) и она не относится к какому-либо отдельному слою, таким образом, продифференцировав (4) по
yj , имеем:
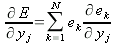 | (26) |
Опять применяем правило цепочки:
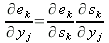 | (27) |
Уравнение (3) можно расписать:
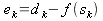 | (28) |
тогда
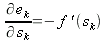 | (29) |
Сигнал, поступающий на
k-й нейрон, определяется выходами нейронов предыдущего слоя и синапсами данного нейрона (как было указано в (1) для
j-го нейрона):
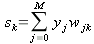 | (30) |
Продифференцируем это уравнение по
yj :
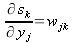 | (31) |
Теперь подставим в (26) по-очереди выражения, полученные в (27), (28) и (31):
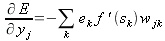 | (32) |
Заметим, здесь один из множителей был расписан ранее в (23). Заменим его:
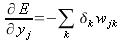 | (33) |
Подставляя это выражение в (25), окончательно имеем:
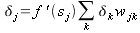 | (34) |
Получилась рекуррентная формула для вычисления локальных градиентов для всех скрытых слоев на основе ранее вычисленных значений
d для вышележащего слоя.
Теперь о практической реализации. Порядок действий следующий.
1. Инициализировать веса небольшими случайными значениями. Слишком малые значения затянут процесс обучения, большие приведут к насыщению нейронов и вызовут паралич сети. Хорошей идеей по подбору порядка весов может быть описанная в [3] , согласно которой для веса устанавливается случайное значение по следующему правилу:
где
L – число нейронов предыдущего слоя, а с учетом формального входа, надо взять
L + 1. Стоит отметить, такой выбор хорош для сигмоидных функций, для гауссовых кривых веса на смещениях следует брать большими.
2. Подать на вход сети один из примеров обучающего набора (выбирать примеры из набора рекомендуется в случайном порядке). Рассчитать выходы нейронов по формулам (1) и (2):
Здесь же желательно вычислить производные и сохранить в массивах для последующего использования. Особенно полезно это при использовании несигмоидных функций, где производная не может быть вычислена только через значение функции.
3. Вычислить
d для всех нейронов выходного слоя по формуле (23):
4. Вычислить
d для нейронов скрытых слоев по формуле (34):
5. Рассчитать все коррекции весов
Dwij по формуле (22):
6. Скорректировать веса:
7. Повторить действия пунктов 2-6 по оставшимся обучающим примерам. Так будет завершена эпоха.
8. Теперь можно оценить ошибку сети (формула (5)):
И, если желаемая точность достигнута, завершить процесс обучения, иначе перейти к пункту 2.
Достоинства алгоритма
1. Алгоритм обоснован теоретически, относительно прост в реализации.
2. Обладает некоторой способностью вырываться из локальных минимумов (при on-line коррекции). Чем больше коэффициент скорости обучения, тем более глубокие ямы могут быть пройдены.
3. В классическом варианте используется только один коэффициент для настройки.
Проблемы алгоритма обратного распространения
1. Несмотря на то, что данный алгоритм имеет хорошее теоретическое обоснование, его сходимость, вообще говоря, не гарантируется.
2. Скорость процесса обучения сильно зависит от выбора коэффициента
h. При его увеличении скорость решения не всегда возрастает. Для каждой задачи и в каждом отдельном случае он выбирается индивидуально. Если коэффициент слишком велик, алгоритм расходится.
3. Алгоритм склонен к застреванию в локальных минимумах (наиболее этому подвержен алгоритм при пакетной (batch) коррекции. Практические задачи и не ставят целью нахождения глобального минимума, к тому же широкий локальный предпочтительнее узкого глобального минимума.
Небольшой дополнением алгоритма можно достичь значительного увеличения скорости обучения, но это, как говорится, совсем другая история, вернее, тема отдельной статьи, там и поговорим о возможных модификациях backprop.
Список литературы
1. Короткий С. Нейронные сети: алгоритм обратного распространения.
2. Haykin Simon. Neural Networks.
3. Воронцов К. В. Лекции по искусственным нейронным сетям – 2005.
4. Заенцев И. Нейронные сети: основные модели. Воронеж (1999)
5. Riedmiller Martin. Advanced Supervised Learning In Multi-Layer Perceptrons – From Backpropagation to Adaptive Learning Algorithms. Karlsruhe

